How To Find The Leading Coefficient Of A Polynomial

Permit's encounter how to graph the polynomial office P(ten) = ten³ - x.

Kickoff of all, nosotros utilize Omni'southward polynomial graphing calculator to exercise the work for united states of america. There, we begin by telling what type of a part nosotros accept. In our case, it'due south a cubic polynomial, and then we cull 3 nether "Polynomial degree." That'll show a symbolic representation of such an expression underneath and corresponding variable fields farther down. Looking back at our polynomial role example, we input:

a₃ = 1, a₂ = 0, a₁ = -i, and a₀ = 0.

(Annotation how we have a₂ = 0 and a₀ = 0 since P(10) has no terms with x² or with no x at all. As well, we input a₃ = 1 and a₁ = -1 even though at that place are no numbers in the corresponding places in P(x). That's because, past convention, nosotros don't write 1-s in front of variables. Nevertheless, find that we needed to remember well-nigh the minus in a₁.)

The moment nosotros input the last coefficient, Omni's polynomial graphing calculator will describe the graph, equally well as find the zeros of the polynomial together with its disquisitional points, extrema, and inflection points. Let the states also mention that in example you'd like to run across some other section of the graph than the one presented, you may go into the advanced mode and input a custom interval.

At present let's endeavour to describe the graph ourselves. First of all, we need to notice the zeros of the polynomial, and then we solve the equation P(x) = 0:

ten³ - x = 0

x * (x² - 1) = 0

x * (x - 1) * (10 + one) = 0

We obtained a production which is equal to 0, which means one of its factors must exist goose egg. In other words, nosotros take x = 0, ten - 1 = 0, or x + 1 = 0, which gives u.s.a. 3 solutions: x = 0, x = 1, and x = -1.

Next, we look for disquisitional points. For that, nosotros compute the derivative P'(x) according to the formula from the above section:

P'(x) = (ten³ - x)' = 3x² - 1.

Now, nosotros solve the equation P'(x) = 0:

3x² - 1 = 0

3x² = 1

x² = ⅓

which gives u.s.a. ii solutions (i.eastward., critical points): -^√three/_three ≈ -0.577 and ^√3/_three ≈ 0.577.

Lastly, we depict the graph. Notation that the leading coefficient of the polynomial is positive (i.e., equal to 1), and it's in front of an odd power of 10 (i.e., x³). That means the finish behavior of the polynomial function is as follows:

P(x) goes to plus infinity when x goes to plus infinity; and
P(x) goes to minus infinity when x goes to minus infinity.

In betwixt, the graph must impact the vertical axis in points -1, 0, and 1, and flatten in -0.577 and 0.577. That takes usa to the conclusion that P(x) has a local maximum in x = -0.577 and a local minimum in x = 0.577; it has no inflection points.

All in all, the graph of P(x) = x³ - x looks similar this:

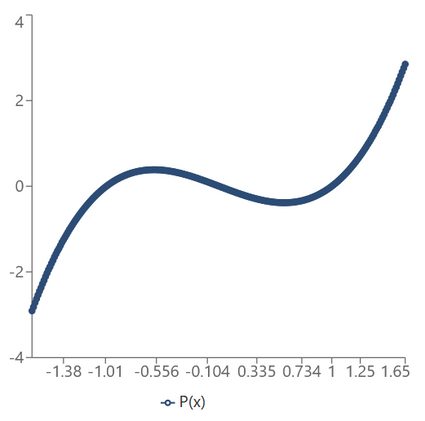
Make certain to experiment with the polynomial graphing calculator to see how different coefficients affect the zeros and the bumps. Also, check out other algebraic tools on the website that tin help in other polynomial-related bug.